Introduction to factors of 18
When you hear the word “factors of 18,” you might think of something mathematical—and you’re absolutely right. Factors are the numbers that divide another number completely, leaving no remainder. In simpler terms, factors of a number are like its building blocks. They tell us what numbers multiply together to form the original number.
For the number 18, these factors are both straightforward and intriguing. While 18 might seem like just another number, diving into its factors can reveal some interesting mathematical properties and real-life applications. Let’s explore these factors and what makes them essential.
What Are the Factors of 18?
At its core, the factors of 18 are the numbers that divide evenly into it. To find these factors, we look for all numbers that can multiply together to equal 18. Here’s a breakdown:
- Start with 1 (because every number is divisible by 1).
- Continue dividing by consecutive numbers until you’ve exhausted all possibilities.
The factors of 18 are: 1, 2, 3, 6, 9, and 18. Let’s take a closer look at how these factors come into play:
- 1 and 18: These are the smallest and largest factors of 18. Multiplying 1 by 18 gives us 18.
- 2 and 9: Divide 18 by 2, and you get 9. These are another pair of factors.
- 3 and 6: Lastly, 3 multiplied by 6 equals 18.
So, the complete factor set for 18 includes both small and large numbers working together in pairs.
Prime Factorization of 18
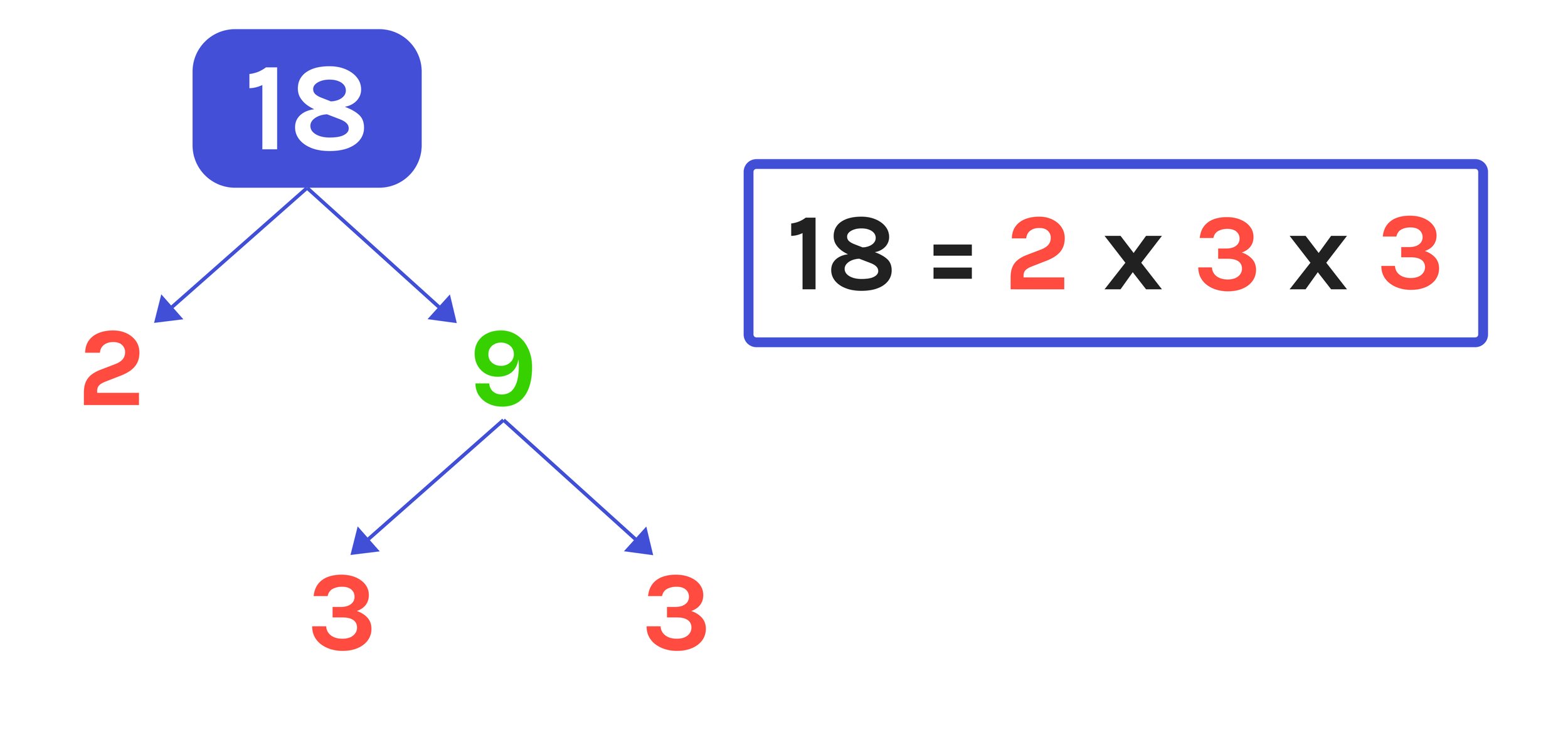
Now, let’s go deeper with prime factorization—breaking 18 down into its prime components. A prime number is one that can only be divided by 1 and itself, like 2, 3, 5, and so on.
For 18:
- Start by dividing it by the smallest prime number, 2. Since 18 is even, it’s divisible by 2:
- 18 ÷ 2 = 9.
- Next, take 9 and divide it by the smallest prime number that fits, which is 3:
- 9 ÷ 3 = 3.
- Finally, divide 3 by itself, as it’s already prime:
- 3 ÷ 3 = 1.
Thus, the prime factorization of 18 is 2 × 3 × 3 or 2 × 3². This breakdown highlights how 18 is constructed from its prime building blocks.
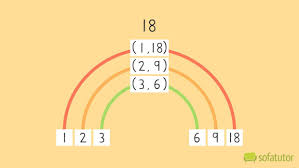
Understanding Pair Factors of 18
Pair factors of a number are sets of two numbers that multiply together to produce the original number. For 18, the pair factors are:
- (1, 18)
- (2, 9)
- (3, 6)
These pairs demonstrate the symmetry in multiplication. Whether you start small and go big (1 × 18) or start in the middle (3 × 6), you’ll always end up with 18. This balance is one reason why factors are so fascinating.
But what about negative numbers? If we include them, the pair factors become:
- (-1, -18)
- (-2, -9)
- (-3, -6)
Negative pair factors work the same way because two negatives multiply to make a positive number.
Real-Life Applications of Factors
You might wonder, “Why should I care about factors in everyday life?” Believe it or not, factors play a significant role in various real-world scenarios. Let’s look at a few examples:
Dividing Resources
Suppose you’re organizing an event and need to split 18 items equally among people. Knowing the factors of 18 helps you figure out your options:
- 2 groups of 9
- 3 groups of 6
- 6 groups of 3
This practical use of factors ensures fairness and efficiency.
Building and Construction
In construction, factors are essential for measurements and layouts. For example, if you’re designing a rectangular floor with an area of 18 square units, the possible dimensions are determined by the factors of 18:
- 1 × 18
- 2 × 9
- 3 × 6
Knowing these dimensions allows for flexibility in design.
Understanding Fractions
Factors simplify fractions. For instance, if you’re working with the fraction 18/36, you can reduce it by dividing both the numerator and denominator by 18 (a common factor):
- 18 ÷ 18 = 1
- 36 ÷ 18 = 2
So, 18/36 simplifies to 1/2.
Fun Facts About the Number 18
Numbers often carry interesting trivia, and 18 is no exception. Here are some fun facts:
- Lucky Number: In many cultures, 18 is considered lucky. In Hebrew, the number symbolizes “chai,” meaning life.
- Mathematical Properties:
- 18 is a Harshad number, meaning it’s divisible by the sum of its digits (1 + 8 = 9).
- It’s also an abundant number, as the sum of its proper factors (1 + 2 + 3 + 6 + 9 = 21) exceeds 18.
- Everyday References: Think about an 18-speed bicycle or turning 18 years old—a significant milestone in many cultures.
Common Misconceptions About Factors
Despite their simplicity, factors are often misunderstood. Let’s clear up some common misconceptions:
- Factors vs. Multiples Many confuse factors with multiples. While factors divide a number, multiples are the results of multiplying it by other numbers. For example:
- Factors of 18: 1, 2, 3, 6, 9, 18.
- Multiples of 18: 18, 36, 54, 72, etc.
- Prime Numbers and Factors Some think prime numbers can’t have factors other than 1 and themselves. While this is true, composite numbers like 18 can have multiple factors.
- Negative Factors Negative factors are often overlooked, but they’re just as valid as positive ones.
The Importance of Factors in Education
Understanding factors isn’t just a math exercise; it’s a foundational concept that builds problem-solving skills. Whether in elementary school or advanced mathematics, factors teach:
- Critical Thinking: Analyzing numbers to find factors strengthens logical reasoning.
- Number Sense: Factors help students grasp relationships between numbers.
- Preparation for Advanced Topics: Concepts like prime factorization lay the groundwork for algebra and beyond.
Conclusion:
Exploring the factors of 18 reveals a world of mathematical wonder. From simple division to prime factorization, these numbers tell a story of balance and structure. Whether applied in real life or studied for academic purposes, factors are indispensable.
Next time you encounter the number 18, take a moment to appreciate its factors. They’re more than just numbers—they’re the building blocks of math and life itself.